Лабораторна робота №8
Мета
Опанувати теоретичні основи символьних обчислень мовами функціонального програмування. Розробити програми символьного диференціювання та реалізації арифметики поліномів.
Опанувати теоретичні основи символьних обчислень мовами функціонального програмування. Розробити програми символьного диференціювання та реалізації арифметики поліномів.
Написати програму, яку визначає інтервали зростання та спадання функції, яка задана алгебраїчним виразом, що містить усі арифметичні операції (+, –, *, /), зведення у степінь та тригонометричні функції tg(x), ctg(x). Для пошуку інтервалів зростання та спадання функції використати першу та другу похідні від функції одної змінної.
Для розв'язку завдання було обрано мову Scheme та середовище DrRacket. Основними критеріями, за якими було зроблено вибір, є:
Наявність доволі великої кількості довідникових джерел інформації з синтаксису та поведінки даної мови. Це, в свою чергу, забезпечено й тим, що дана мова є діалектом розповсюдженої мови - LISP.
Відносна простота даної мови у засвоєнні, а середовища - використані, завдяки зрозумілому мінімалістичному користувацьому інтерфейсу, що надає найпоширеніший функціонал для написання та відлагоджування коду.
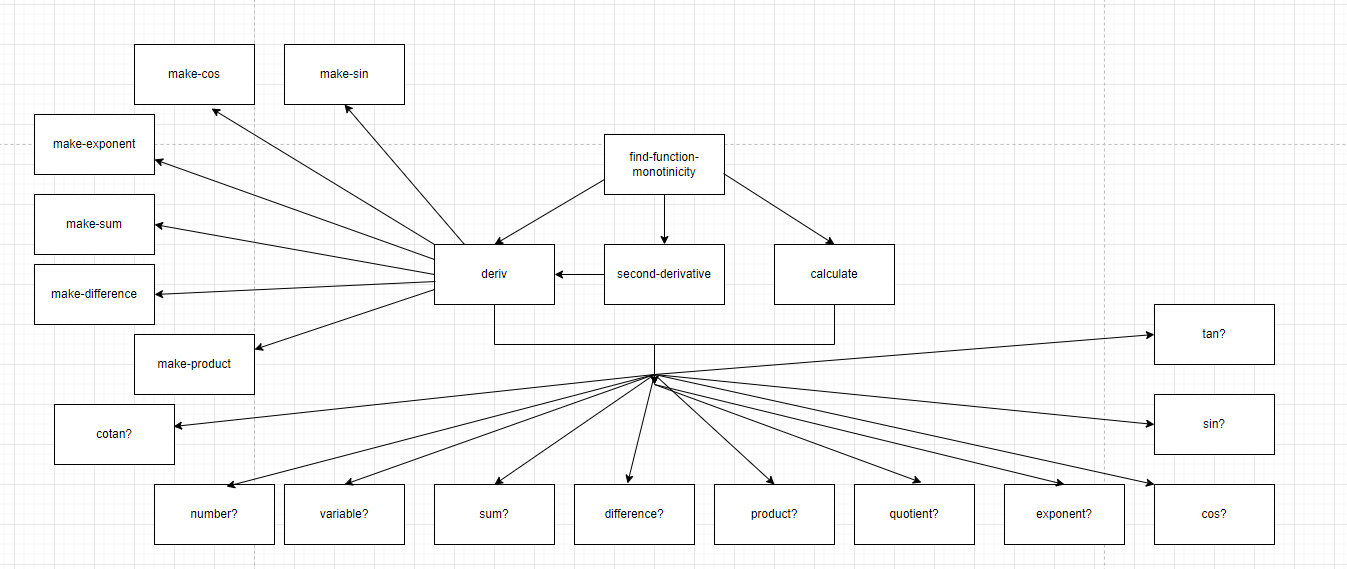
#lang racket
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 8, завдання 14
; функція визначення того, чи є вираз змінною
(define (variable? x) (symbol? x))
; функція визначення того, чи є аргументи однаковою змінною
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2)))
; функції створення виразів, відповідно, суми, різниці. добутку, частки, степеню, косинуса, синуса
(define (make-sum a1 a2) (list '+ a1 a2))
(define (make-difference a1 a2) (list '- a1 a2))
(define (make-product m1 m2) (list '* m1 m2))
(define (make-quotient d1 d2) (list '/ d1 d2))
(define (make-exponent p1 p2) (list 'expt p1 p2))
(define (make-cos t1) (list 'cos t1))
(define (make-sin t1) (list 'sin t1))
; функція визначення того, чи є вираз сумою
(define (sum? x)
(and (pair? x) (eq? (car x) '+)))
; функція визначення того, чи є вираз відніманням
(define (difference? x)
(and (pair? x) (eq? (car x) '-)))
; функця отримання першого аргументу виразу
(define (addend s) (cadr s))
; функця отримання другого аргументу виразу
(define (augend s) (caddr s))
; функція визначення того, чи є вираз добутком
(define (product? x)
(and (pair? x) (eq? (car x) '*)))
; функція визначення того, чи є вираз часткою
(define (quotient? x)
(and (pair? x) (eq? (car x) '/)))
; функція визначення того, чи є вираз піднесенням до степеня
(define (exponent? x)
(and (pair? x) (eq? (car x) 'expt)))
; функція визначення того, чи є вираз косинусом
(define (cos? x)
(and (pair? x) (eq? (car x) 'cos)))
; функція визначення того, чи є вираз синусом
(define (sin? x)
(and (pair? x) (eq? (car x) 'sin)))
; функція визначення того, чи є вираз тангенсом
(define (tan? x)
(and (pair? x) (eq? (car x) 'tan)))
; функція визначення того, чи є вираз котангенсом
(define (cotan? x)
(and (pair? x) (eq? (car x) 'cotan)))
; функця отримання першого аргументу виразу
(define (multiplier p) (cadr p))
; функця отримання другого аргументу виразу
(define (multiplicand p) (caddr p))
; функця отримання першого аргументу виразу
(define (dividend p) (cadr p))
; функця отримання другого аргументу виразу
(define (divisor p) (caddr p))
; функця отримання першого аргументу виразу
(define (power-base p) (cadr p))
; функця отримання другого аргументу виразу
(define (power-exponent p) (caddr p))
; функця отримання першого аргументу виразу
(define (tan-base p) (cadr p))
; функця отримання першого аргументу виразу
(define (cotan-base p) (cadr p))
; функця отримання похідної виразу
(define (deriv exp var)
(cond
; похідною числа є 0
[(number? exp) 0]
; похідною змінної, за якою відбувається диференціювання, є 1, інкаше - 0
[(variable? exp)
(if (same-variable? exp var) 1 0)]
; похідною суми є сума похідних
[(sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)
)
]
; похідною різниці є різниця похідних
[(difference? exp)
(make-difference (deriv (addend exp) var)
(deriv (augend exp) var)
)
]
; для похідної добутку користуємось формулою (uv)' = u'v + uv'
[(product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))
)
]
; для похідної часткм користуємось формулою (u/v)' = (u'v - uv')/(v^2)
[(quotient? exp)
(make-quotient
(make-difference
(make-product (deriv (dividend exp) var)
(divisor exp))
(make-product (dividend exp)
(deriv (divisor exp) var))
)
(make-product (divisor exp) (divisor exp))
)
]
; для похідної піднесення до степеня користуємось формулою (u^n)' = n*(u^(n-1))*u'
[(exponent? exp)
(make-product
(make-product (power-exponent exp)
(make-exponent (power-base exp)
(make-difference (power-exponent exp) '1)
)
)
(deriv (power-base exp) var)
)
]
; для похідної тангенса користуємось формулою tg(u)' = u'*(-1/(cos(u)^2))
[(tan? exp)
(make-product
(deriv (tan-base exp) var)
(make-exponent (make-cos (tan-base exp)) '-2)
)
]
; для похідної косинуса користуємось формулою cos(u)' = u'*(-1)*sin(u)
[(cos? exp)
(make-product
(deriv (tan-base exp) var)
(make-product
'-1
(make-sin (tan-base exp))
)
)
]
; для похідної синуса користуємось формулою sin(u)' = u'*cos(u)
[(sin? exp)
(make-product
(deriv (tan-base exp) var)
(make-cos (tan-base exp))
)
]
; для похідної котангенса користуємось формулою ctg(u)' = u'*(1/(sin(u)^2))
[(cotan? exp)
(make-product
(deriv (tan-base exp) var)
(make-product
'-1
(make-exponent (make-sin (tan-base exp)) '-2)
)
)
]
[else
(display "unknown expression type - DERIV" )]
)
)
; функція обчислення чисельного значення похідних
(define (calculate exp var var-value)
(cond
; якщо вираз - число, повернути його значення
[(number? exp) exp]
; якщо вираз - змінна, повернути задане її значення
[(variable? exp) var-value]
; якщо вираз - сума, повернути суму значень доданків
[(sum? exp)
(+ (calculate (addend exp) var var-value)
(calculate (augend exp) var var-value)
)
]
; якщо вираз - різниця, повернути різницю значень операндів
[(difference? exp)
(- (calculate (addend exp) var var-value)
(calculate (augend exp) var var-value)
)
]
; якщо вираз - добуток, повернути добуток значень операндів
[(product? exp)
(* (calculate (multiplier exp) var var-value)
(calculate (multiplicand exp) var var-value)
)
]
; якщо вираз - ділення, повернути частку значень операндів
[(quotient? exp)
(/ (calculate (dividend exp) var var-value)
(calculate (divisor exp) var var-value)
)
]
; якщо вираз - піднесення до степеня, повернути значення першого виразу, піднесене до степеня - значення другого виразу
[(exponent? exp)
(expt (calculate (power-base exp) var var-value)
(calculate (power-exponent exp) var var-value)
)
]
; якщо вираз - косинус, повернути косинус внутрішнього виразу
[(cos? exp)
(cos (calculate (tan-base exp) var var-value)
)
]
; якщо вираз - синус, повернути синус внутрішнього виразу
[(sin? exp)
(sin (calculate (tan-base exp) var var-value)
)
]
; якщо вираз - тангенс, повернути тангенс внутрішнього виразу
[(tan? exp)
(tan (calculate (tan-base exp) var var-value)
)
]
; якщо вираз - котангенс, повернути котангенс внутрішнього виразу
[(cotan? exp)
(/ 1 (tan (calculate (tan-base exp) var var-value))
)
]
[else
(display "unknown expression type - DERIV" )]
)
)
; функція для обчислення другої похідної як похідної від похідної
(define (second-derivative exp var)
(deriv (deriv exp var) var)
)
; функція для обчислення і виведення кінцевих значень
(define (find-function-monotinicity exp variable-value)
(begin
(define first-deriv (deriv exp 'x))
(define second-deriv (second-derivative exp 'x))
(define first-deriv-value (calculate first-deriv 'x variable-value))
(define second-deriv-value (calculate second-deriv 'x variable-value))
(display "The function's first derivative: \n")
(display first-deriv)
(newline)
(display "===========================\n")
(display "The function's second derivative: \n")
(display second-deriv)
(newline)
(display "===========================\n")
(display "The function's first derivative's value: ")
(display first-deriv-value)
(newline)
(display "The function's second derivative's value: ")
(display second-deriv-value)
(newline)
(display "===========================\n")
(cond [(> first-deriv-value 0)
(display "The function is increasing in the given point.\n")]
[(< first-deriv-value 0)
(display "The function is decreasing in the given point.\n")]
[(> second-deriv-value 0)
(display "The given point is a point of minimum.\n")]
[(< second-deriv-value 0)
(display "The given point is a point of minimum.\n")]
)
)
)
(define expression '(/ x (+ (* 2 x) (cotan x))))
(find-function-monotinicity expression 1)

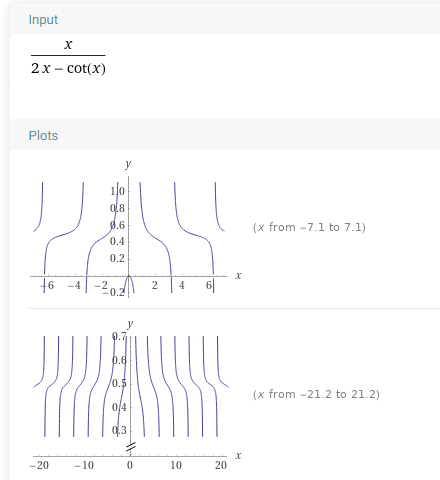
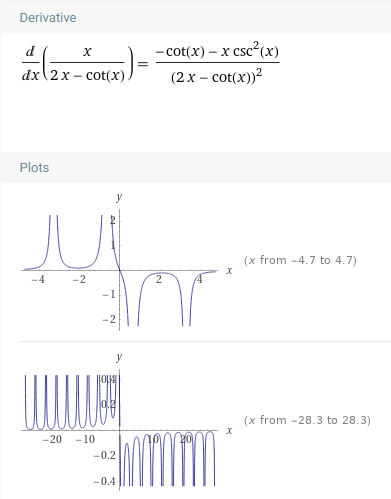
Правильність виконання задачі було перевірено для функції x / (2x - ctg(x)) в точці x = 2. Нижче наведено скріншоти засобу "WolframAlpha", що демонструють графіки, відповідно, самої функції, її першої та другої похідної. Як бачимо з рисунку, в точці 2 графік спадає, а перша похідна має від'ємне значення. Дійсно, програматично було отримано значення першої похідної: -0.09870020918752292 та висновок про те, що графік у точці спадає - що співпадає з очікуваними результатами.
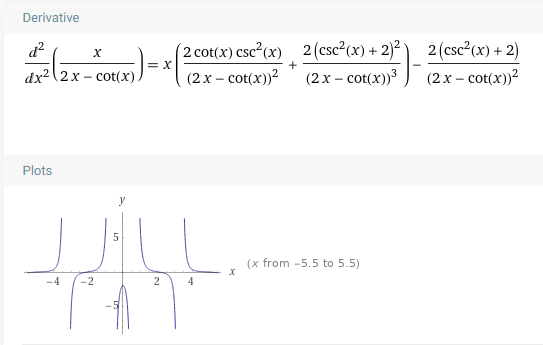
В лабораторній роботі було реалізовано завдання, що передбачає символьні обчислення першої та другої похідної виразів, що містять задані функції.
Основні труднощі виникли при реалізації пошуку інтервалів зростання чи спадання. Так, оскільки саме така постановка задачі не розглядалась на жодному з курсів за всі 4 роки навчання, дана задача виадась непідсильною. Натомість, було реалізовано обчислення значення першої та другої похідної у точці та, як наслідок, визначення характеру монотонності функції в ній.