Опанувати теоретичні основи обробки структур типу векторів і матриць, стеків та черг мовами функціонального програмування та розробити програми їх реалізації.
14.1. Створити вектор чисел. Знайти найбільший серед від’ємних та найменший серед додатних елементів вектору. Вивести вектор, значення знайдених елементів та їх індекси.
14.2. Створити стек натуральних чисел. Вибрати зі стеку числа, які не повторюються і записати їх у чергу. Надрукувати стек і чергу вибраних елементів.
Для розв'язку завдання було обрано мову Scheme та середовище DrRacket. Основними критеріями, за якими було зроблено вибір, є:
Наявність доволі великої кількості довідникових джерел інформації з синтаксису та поведінки даної мови. Це, в свою чергу, забезпечено й тим, що дана мова є діалектом розповсюдженої мови - LISP.
Відносна простота даної мови у засвоєнні, а середовища - використані, завдяки зрозумілому мінімалістичному користувацьому інтерфейсу, що надає найпоширеніший функціонал для написання та відлагоджування коду.
#lang racket
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 6, завдання 14.1
; фунекція пошуку найбільшого від'ємого числа
(define (find-maximum-negative vector)
(find-maximum-negative-internal vector 0)
)
; внутрішня фунекція пошуку найбільшого від'ємого числа
(define (find-maximum-negative-internal vector index)
(cond [(< index (vector-length vector))
(begin
(define current-number (vector-ref vector index))
(cond
; якщо максимальне число не визначене, а поточне число - від'ємне, присвоїти його значення максимсальному
[(and (not (pair? maximum-negative)) (< current-number 0))
(set! maximum-negative (cons index current-number))
]
; якщо максимальне число визначене, а поточне число - від'ємне і більше за нього, присвоїти його значення максимсальному
[(and (pair? maximum-negative) (< (cdr maximum-negative) current-number) (< current-number 0))
(set! maximum-negative (cons index current-number))
]
)
(find-maximum-negative-internal vector (+ 1 index))
)
]
)
)
; фунекція пошуку найменшого додатного числа
(define (find-minimum-positive vector)
(find-minimum-positive-internal vector 0)
)
; внутрішня фунекція пошуку найменшого додатного числа
(define (find-minimum-positive-internal vector index)
(cond [(< index (vector-length vector))
(begin
(define current-number (vector-ref vector index))
(cond
; якщо мінімальне число не визначене, а поточне число - дадатне, присвоїти його значення мінімальному
[(and (not (pair? minimum-positive)) (> current-number 0))
(set! minimum-positive (cons index current-number))
]
; якщо мінімальне число визначене, а поточне число - дадатне і менеше за нього, присвоїти його значення мінімальному
[(and (pair? minimum-positive) (> (cdr minimum-positive) current-number) (> current-number 0))
(set! minimum-positive (cons index current-number))
]
)
(find-minimum-positive-internal vector (+ 1 index))
)
]
)
)
; функція друку результатів
(define (print-results)
(begin
(display "The initial vector: ")
(display number-vector)
(display "\n")
(cond [(pair? maximum-negative)
(begin
(display "The maximum negative number: ")
(display (cdr maximum-negative))
(display ". Its index within the list: ")
(display (car maximum-negative))
)
]
; Окремий випадок, якщо від'ємних чисел немає взагалі
[else
(begin
(display "Could not find the maximum negative number as there are no negative numbers in the vector.")
)
]
)
(display "\n")
(cond [(pair? minimum-positive)
(begin
(display "The minimum positive number: ")
(display (cdr minimum-positive))
(display ". Its index within the list: ")
(display (car minimum-positive))
)
]
; Окремий випадок, якщо додатних чисел немає взагалі
[else
(begin
(display "Could not find the minimum positive number as there are no positive numbers in the vector.")
)
]
)
)
)
(define number-vector #(-12 -32 -5 -3 -2 -6 -15 -4 -16))
(define maximum-negative '())
(define minimum-positive '())
(find-maximum-negative number-vector)
(find-minimum-positive number-vector)
(print-results)
#lang racket
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 6, завдання 14.2
; функція пошуку елемента за його індексом
(define (get-list-element elements n)
(if (= n 1)
(car elements)
(get-list-element (cdr elements) (- n 1 ))
)
)
; функція вилучення першого елемента з черги
(define (pop-queue)
(begin
(define popped-number (car queue))
(display "Removing ")
(display popped-number)
(display " from the queue.\n")
(set! queue (cdr queue))
(display "Current queue state: ")
(display queue)
(display "\n")
popped-number
)
)
; функція додавання останнього елемента в чергу
(define (push-queue n)
(begin
(display "Adding ")
(display n)
(display " to the queue.\n")
(set! queue (append queue (list n)))
(display "Current queue state: ")
(display queue)
(display "\n")
)
)
; функція вилучення першого елемента зі стеку
(define (pop-stack)
(begin
(define popped-number (get-list-element stack (length stack)))
(display "Removing ")
(display popped-number)
(display " from the stack.\n")
(set! stack (pop-stack-inner stack))
(display "Current stack state: ")
(display stack)
(display "\n")
popped-number
)
)
; функція отримання стеку без останнього його елемента
(define (pop-stack-inner current-stack)
(cond [(> (length current-stack) 1)
(append (list (car current-stack)) (pop-stack-inner (cdr current-stack)))
]
[else
'()
]
)
)
; функція додавання останнього елемента в стек
(define (push-stack n)
(begin
(display "Adding ")
(display n)
(display " to the stack.\n")
(set! stack (append stack (list n)))
(display "Current stack state: ")
(display stack)
(display "\n")
)
)
; функція, що підраховує кількість елементів, що відповідають заданому числу в списку
(define (number-of-occurences n current-list count)
(cond
[(not (null? current-list))
; якщо поточний елемент відповідає заданому, збільшити лічильник на 1, інакше з поточним лічильнимнком перевіряти наступні елементи
(if (= n (car current-list))
(number-of-occurences n (cdr current-list) (+ 1 count))
(number-of-occurences n (cdr current-list) count)
)
]
[else
count
]
)
)
; функція вилучення елементів стеку і заповнення проміжного списку
(define (empty-the-stack)
; якщо стек вже порожній, вивести відповідне повідомлення
(cond [(empty? stack)
(begin
(display "The resulting stack is: ")
(display stack)
(display "\n")
)
]
; інакше прибрати наступний елемент
[else
(begin
(define current-number (pop-stack))
(set! temp-list (append temp-list (list current-number)))
(empty-the-stack)
)
]
)
)
; функція наповнення вихідної черги, спираючись на список проміжних значень
(define (fill-the-queue source)
; Якщо всі еоементи вже обійшли, вивести відповідне повідомлення
(cond [(empty? source)
(begin
(display "The resulting queue is: ")
(display queue)
(display "\n")
)
]
[else
(begin
(define current-number (car source))
; Якщо поточний елемент зустрічається у вихідному списку лише раз, записати його у чергу
(cond [(= ( number-of-occurences current-number temp-list 0) 1)
(push-queue current-number)
]
; Інакше вивести повідомлення про наявність дублікатів
[else
(begin
(display "Skipping ")
(display current-number)
(display " as it is used more than once.\n")
)
]
)
; Продовжити обхід для решти елементів
(fill-the-queue (cdr source))
)
]
)
)
(define queue (list))
(define stack (list))
(define temp-list (list))
(push-stack 1)
(push-stack 2)
(push-stack 1)
(push-stack 4)
(push-stack 5)
(push-stack 3)
(push-stack 7)
(push-stack 11)
(push-stack 3)
(push-stack 12)
(push-stack 8)
(push-stack 1)
(empty-the-stack)
(fill-the-queue temp-list)
Завдання 14.1 Правильність формування початкового списку було перевірено для вектору: (-12 -32 -5 -3 -2 -6 15 -4 -16). Так, самостійно було виконано завдання, та визначено, що найбільше від'ємне число - -2 - знаходиться за індексом 4 (починаючи з 0), а найменше додатнє - 15 - за інексом 6. Отриманs насправді результати збігаються з передбачуваними..
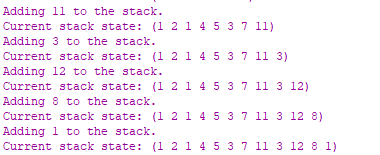
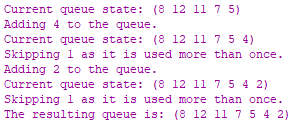
Завдання 14.2 Правильність виконання програми було перевірено для послідовності стеку, що було заповнено елементами: (1 2 1 4 5 3 7 11 3 12 8 1). Так, було визначено список елементів що повторюються, а саме: (1 3), отже передбачувана черга повинна містити елементи (2 4 5 7 11 12 8), а з врахуванням порядку вибування елементів зі стеку, кінцевий вигляд черги має бути: (8 12 11 7 5 4 2). Отриманий насправді результат відповідає очікуваному.
В лабораторній роботі було реалізовано обидва завдання, що передбачають маніпуляції з векторами, а також - списками та стеками, реалізованими через списки.
Певні труднощі виникли лише при програмній реалізації завдання 14.2. Так, через неуважність при прочитанні завдання, спочатку було створено реалізовацію, що додавала у чергу всі унікальні елементи стеку. Інакше кажучи, якщо в стеку є 2 ідентичних елементи, такий елемент додався б лише раз. Згодом цю проблему було помічено та усунуто, і результуюча імплементація була доволі триваільною, попри додаткові витрати часу.