Розв’язати нелінійні рівняння та здійснити чисельне інтегрування функцій наближеними методами, використовуючи мови функціонального програмування та lambda, let та set! форми.
14.1. Знайти корені нелінійного рівняння виду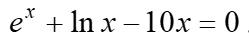 
. Пошук наближеного значення хоча б одного кореня рівняння f(x) = 0 на відрізку [a; b] здійснювати методами простої ітерації та дотичних. Значення a, b інтервалу вибрати самостійно. Порівняти результати розв’язків двома методами.
14.2. Написати процедури для обчислити інтеграла за формулами прямокутників і Сімпсона. Порівняти результати обчислення.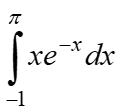 
Для розв'язку завдання було обрано мову Scheme та середовище DrRacket. Основними критеріями, за якими було зроблено вибір, є:
Наявність доволі великої кількості довідникових джерел інформації з синтаксису та поведінки даної мови. Це, в свою чергу, забезпечено й тим, що дана мова є діалектом розповсюдженої мови - LISP.
Відносна простота даної мови у засвоєнні, а середовища - використані, завдяки зрозумілому мінімалістичному користувацьому інтерфейсу, що надає найпоширеніший функціонал для написання та відлагоджування коду.
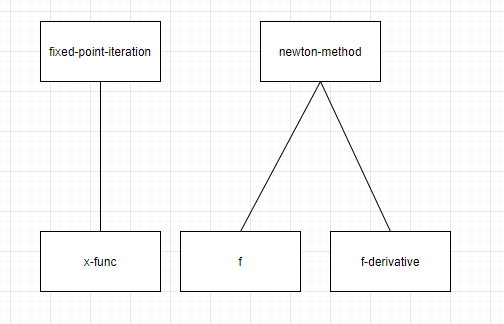
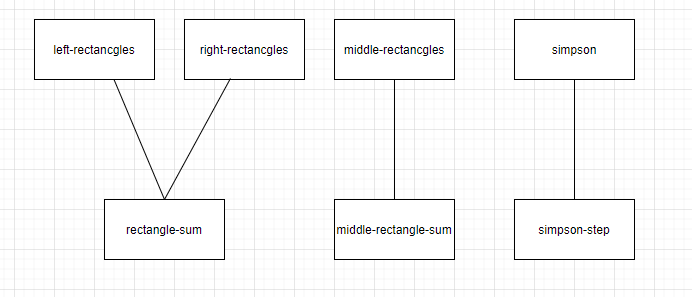
#lang racket
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 3, завдання 14.1
; точність, за якою визначається закінчення процедури
(define error 1e-5)
; f(x) = e^x + 10x
(define (f x)
(+ (exp x) (* 10 x))
)
; X = e^x / (-10)
(define (x-func x)
(/ (exp x) -10)
)
;f'(x) = e^x + 10
(define (f-derivative x)
(+ (exp x) 10)
)
; Процедура обчислення кореня методом простої ітерації
(define (fixed-point-iteration current-x)
; Обчислення наступного значення X, спираючись на канонічне рівняння для поточного
(let ((next-x (x-func current-x)))
; Якщо різниця між поточним та наступним X менша за похибку, рекурсія припиняється, і повертається поточне значення
(if (< (abs (- next-x current-x)) error)
current-x
; Інакше процедура рекурсивно обчислює наступне наближене значення, використовуючи нове значення як поточне
(fixed-point-iteration next-x)
)
)
)
; Процедура обчислення кореня методом дотичних
(define (newton-method current-x)
; Наступне значення X обчислюється як xk+1 = xk - (f(xk) / f'(xk))
(let ((next-x (- current-x (/(f current-x) (f-derivative current-x)))))
; Якщо різниця між поточним та наступним X менша за похибку, рекурсія припиняється, і повертається поточне значення
(if (< (abs (- next-x current-x)) error)
current-x
; Інакше процедура рекурсивно обчислює наступне наближене значення, використовуючи нове значення як поточне
(newton-method next-x)
)
)
)
(define fixed-point-iteration-solution (fixed-point-iteration 4))
(define newton-solution (newton-method 4))
(define solution-difference (abs (- fixed-point-iteration-solution newton-solution)))
(display "Solution using the Fixed-Point Iteration method: ")
(display fixed-point-iteration-solution)
(display "\n")
(display "Solution using the Newton method: ")
(display newton-solution)
(display "\n")
(display "Absolute difference between the solutions: ")
(display solution-difference)
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 3, завдання 14.2
; Початок проміжку
(define start -1)
; Кінець проміжку
(define end pi)
; Процедура обчислення значення заданої функції
(define (f x)
(* x (exp (* -1 x)))
)
; Процедура обчислення інтегралу за методом правих прямокутників
(define (right-rectangles a b n)
; Визначення величини кроку
(let* ([step (/(- b a)n)]
; Обчислення суми значень f(x), на проміжку i=1...n
[sum (rectangle-sum (+ a step) b step 0)])
; Повернення кінцевого значення як добутку кроку на суму значень функції
(* step sum)
)
)
; Процедура обчислення інтегралу за методом лівих прямокутників
(define (left-rectangles a b n)
; Визначення величини кроку
(let* ([step (/(- b a)n)]
; Обчислення суми значень f(x), на проміжку i=0...n-1
[sum (rectangle-sum a (- b step) step 0)])
; Повернення кінцевого значення як добутку кроку на суму значень функції
(* step sum)
)
)
; Процедура обчислення інтегралу за методом середніх прямокутників
(define (middle-rectangles a b n)
; Визначення величини кроку
(let* ([step (/(- b a)n)]
; Обчислення суми значень f((xk + xk+1)/2), для точок на проміжку i=0...n-1
[sum (middle-rectangle-sum a (- b step) step 0)])
; Повернення кінцевого значення як добутку кроку на суму значень функції
(* step sum)
)
)
; Процедура обчислення суми значень f(x) для всіх x на заданому проміжку
(define (rectangle-sum current-x end-x step current-sum)
; Поточне значення визначається як f(x)
(let ((current-f (f current-x)))
; Якщо x вийшло за заданий проиіжок, повертається сума, отримана попереднім викликом процедури
(if (> current-x end-x)
current-sum
; Інакше рекурсивно обчислюється сума для подальших x на проміжку
(rectangle-sum (+ current-x step) end-x step (+ current-sum current-f))
)
)
)
; Процедура обчислення суми значень f((xk + xk+1)/2) для всіх x на заданому проміжку
(define (middle-rectangle-sum current-x end-x step current-sum)
; Поточне значення визначається як f(x + step / 2)
(let ((current-f (f (+ current-x (/ step 2)))))
; Якщо x вийшло за заданий проиіжок, повертається сума, отримана попереднім викликом процедури
(if (> current-x end-x)
current-sum
; Інакше рекурсивно обчислюється сума для подальших x на проміжку
(middle-rectangle-sum (+ current-x step) end-x step (+ current-sum current-f))
)
)
)
; Процедура для обчислення інтегралу за методом Сімпсона на заданому проміжку
(define (simpson a b n)
; Визначення величини кроку
(let* ([step (/ (- b a) n)]
; Обчислення суми виразу, наведеного у формулі, для всіх x на проміжку від a до b
[sum (simpson-step a b step 0)])
; Повернення кінцевого результату як вищезгадана сума, помножена на третину кроку
(* (/ step 3) sum)
)
)
; Процедура для обчислення суми виразу, наведеного у формулі методу Сімпсона
(define (simpson-step current-x end-x step current-sum)
; Визначення величини в заданій точці
(let* ([start-f (f current-x)]
; Визначення величини в точці, отриманій додаванням кроку до заданої
[middle-f (f (+ current-x step))]
; Визначення величини в точці, отриманій додаванням 2 величин кроку до заданої
[end-f (f (+ current-x step step))]
; Визначення величини суми для поточної ітерації
[step-sum (+ start-f (* 4 middle-f) end-f)])
; Якщо x вийшло за заданий проиіжок, повертається сума, отримана попереднім викликом процедури
(if (> current-x end-x)
current-sum
; Інакше рекурсивно обчислюється сума для подальших x на проміжку
(simpson-step (+ current-x step step) end-x step (+ current-sum step-sum))
)
)
)
(define steps 1000)
(define right-rectangle-solution (right-rectangles start end steps))
(define left-rectangle-solution (left-rectangles start end steps))
(define middle-rectangle-solution (middle-rectangles start end steps))
(define simpson-solution (simpson start end steps))
(display "Solution using the Right Rectangle method: ")
(display right-rectangle-solution)
(display "\n")
(display "Solution using the Left Rectangle method: ")
(display left-rectangle-solution)
(display "\n")
(display "Solution using the Middle Rectangle method: ")
(display middle-rectangle-solution)
(display "\n")
(display "Solution using the Simpson method: ")
(display simpson-solution)
Завдання 14.1 Правильність виконання процедури було перевірено для початкового наближення 4 та точності 1e-5. Так, згідно з онлайн-калькулятором "Wolfram", значення виразу в даній точці становить -0.0912765. Водночас, реалізована процедура методу простої ітерації повертає результат -0.09126995185428846, а методу Ньютона - -0.09127652584007065. Як бачимо, отримане методом Ньютона значення більше відповідає дійсності, проте й метод простої ітерації має доволі високу точність: різниця між отриманими результатами становить лише 6e-6.
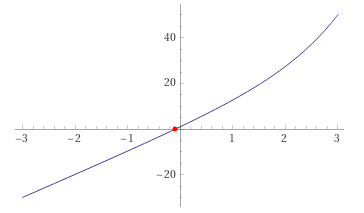
Завдання 14.2 Правильність виконання процедури було перевірено для кількості проміжків - 1000. Так, згідно з онлайн-калькулятором "Wolfram", значення інтегралу становить -0.17897. Згідно з наведеним вище скріншотом результатів бачимо, що найбільшу точність має метод Сімпсона з результатом: -0.1789744. Водночас, відносно високу точність в даній ситуації має і метод середніх прямокутників, в той час як методи правих та лівих - мають похибку в близько 0.006
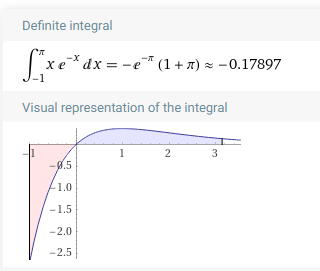
В лабораторній роботі було реалізовано обидва завдання, що передбачають розв’язання нелінійних рівнянь та чисельного інтегрування функцій згідно з заданими користувачем точністю та проміжком рочаткового наближення розв'язку або ж кількістю ділянок, на які ділиться проміжок інтегрування.
Труднощі постали при програмній реалізації завдання 14.1, зокрема - через те, що для заданого в умові завдання виразу на проміжку, на якому міститься чисельний розв'язок, не виконуються умови збіжності ні одного з методів.
Попри загальну простоту розв'язку завдання 14.2, виникли труднощі з архітектурою додатку. Так, як показує досвід, логіка обчислення проміжних результатів на окремомій ітерації є доволі подібною для всіх методів прямокутників, через що було вчинено спробу абстрагувати імплементацію з метою перевикористання спільної прцоедури для всіх методів. На жаль, врешті-решт, спільну імплементацію використовують лише методи правих та лівих прямокутників, у той час як середніх - використовує власну імплементацію.