Опанувати теоретичні основи застосування рекурентних співвідношень для обчислення тригонометричних, експоненціальних, степеневих функцій та розробити програми функціональними мовам програмування для обчислення їх значень.
14.1. Обчислити значення функції у, розвинувши функцію у ряд Тейлора. Аргумент х змінюється від -2 до 2 з кроком 0.5. Визначити похибку.
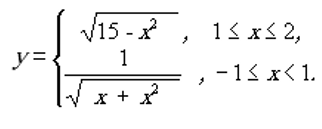
14.2. У трьох видах спорту стартує n осіб. Визначити, скільки існує можливих результатів, якими можуть закінчитися змагання, якщо кожна людина стартує в одному, довільно обраному виді спорту? Під результатом змагання розуміється розподіл місць для всіх спортсменів, що стартують в кожному виді.
Для розв'язку завдання було обрано мову Scheme та середовище DrRacket. Основними критеріями, за якими було зроблено вибір, є:
Наявність доволі великої кількості довідникових джерел інформації з синтаксису та поведінки даної мови. Це, в свою чергу, забезпечено й тим, що дана мова є діалектом розповсюдженої мови - LISP.
Відносна простота даної мови у засвоєнні, а середовища - використані, завдяки зрозумілому мінімалістичному користувацьому інтерфейсу, що надає найпоширеніший функціонал для написання та відлагоджування коду.
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 2, завдання 14.1
; точність, за якою визначається закінчення процедури
(define error 1e-9)
; кількість ітерацій, за якими припиняється процедура, у разі не досягнення бажаної точності
(define max-iterations 1000)
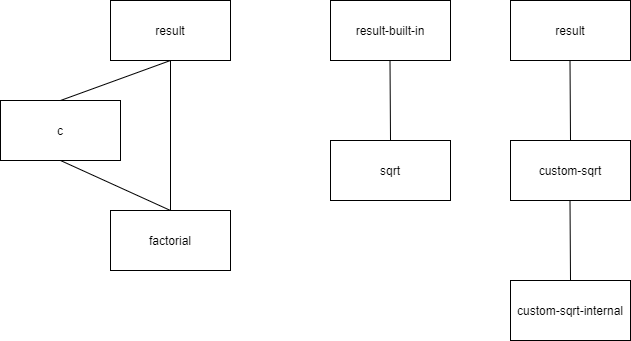
; процедура для обчислення заданої функції, спираючись на вбудовану поцедуру "sqrt"
(define (result-built-in value)
(cond
; перша умова для обчислення значення
[(and(>= value 1)(<= value 2))
(sqrt(- 15 (* value value )))]
; друга умова для обчислення значення
[(and(>= value -1)(< value 1))
(/ 1 (sqrt (+ value (* value value))))]
))
; процедура для обчислення заданої функції, спираючись на власну реалізацію
(define (result value)
(cond
; перша умова для обчислення значення
[(and(>= value 1)(<= value 2))
(custom-sqrt(- 15 (* value value )) 0 0)]
; друга умова для обчислення значення
[(and(>= value -1)(< value 1))
(/ 1 (custom-sqrt (+ value (* value value)) 0 0))]
))
; процедура для обчислення похибки при обчисленні заданої функції, спираючись на вбудовану та власну реалізації
(define (method-difference value)
; значення має повертатись лише для точок, що входять в межі, задані умовою, та для дійсних значень
(cond[(and(not(void? (result-built-in value)))(real? (result-built-in value)))
(abs(- (result value) (result-built-in value)))]
)
)
; процедура для обчислення квадратного кореня, згідно з заданою формулою
(define (custom-sqrt x n previous-member )
; на кожному кроці обчислюється значення поточного члена послідовності
(define current-member (custom-sqrt-internal x n previous-member))
; рекурсія завершується у разі, якщо досягнуто бажану точність, або ж виконано достатню кількість ітерацій
(if (or (< (abs (- previous-member current-member)) error) (> n max-iterations))
; в разі закінчення рекурсії повертається значення поточного члена ряду
current-member
; інакше рекурсивно викликається поточна процедура для наступного члена ряду
(custom-sqrt x (+ n 1) current-member))
)
; внутрішня процедура для обчислення значення поточного члена ряду
(define (custom-sqrt-internal x n previous-member)
; виняткове значення повертається для нульового члена ряду
(if (= n 0)
1
; інакше значення обчислюється згідно з формулою
(* 0.5 (+ previous-member (/ x previous-member)))
)
)
(display "Результат з використанням вбудованої функції:\n")
(map result-built-in (inclusive-range -2 2 0.5))
(display "Результат з використанням власної реалізації:\n")
(map result (inclusive-range -2 2 0.5))
(display "Похибки:\n")
(map method-difference (inclusive-range -2 2 0.5))
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 2, завдання 14.2
; процедура для обчислення факторіалу
(define (factorial value)
; кінцева умова рекурсії - коли задане число є нулем, у випадку чого повертаємо 1
(if (= value 0)
1
; інакше процедура викликається рекурсивно, повертаючи добуток поточного числа та факторіала на 1 меншого
(* value (factorial (- value 1)))
)
)
; процедура обчислення комбінації з повтореннями, спираючись на реалізацію процедури обчислення факторіалу
; в межах завдання за n сприймаємо кількість елементів, що можуть повторюватись, а саме - види спорту (кількість яких - 3)
(define (c n k)
(/(factorial (+ n k -1)) (*(factorial k) (factorial (- n 1))))
)
; процедура обчислення кінцевого результату завдання
; згідно з умовою, обчислюється добуток кількості комбінацій з 3 по n (як кількість варіантів розподілу)
; та факторіал n (як кількість варіантів розподілу спортсменів аза місцями)
(define (result n)
(*(c 3 n) (factorial n))
)
(display "Введіть кількість атлетів:\n")
(define input (read))
;(display (input "спортсменів можна розподілити між 3 видами спорту "(result input) " кількість атлетів:\n"))
(fprintf (current-output-port)
"~a спортсменів можна розподілити між 3 видами спорту ~s способами.\n"
input
(result input))
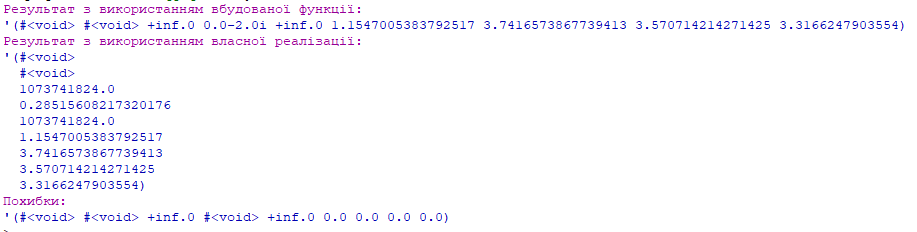
Завдання 14.1 Правильність виконання процедури було перевірено для точки 2. Так, згідно з онлайн-калькулятором "Wolfram", значення виразу в даній точці становить 3.31662479035539984911493273667068. Водночас, вбудована функція sqrt повертає результат 3.3166247903554, а створена реалізація алгоритму - 3.3166247903554. Як бачимо, отримане значення відповідає дійсності з точністю 13 знаків після коми, що перевищує навіть задану програматично точність в 9 знаків.
Завдання 14.2 Правильність виконання процедури було перевірено для вхідних даних: n = 10. Так, скориставшись онлайн-калькулятором для задач з комбінаторики keisan.casio.com, було визначено, що значення кількості комбінацій з повтореннями з 3 по 10 становить 66, а кількість перестановок з 10 - 3628800. Кінцевий результат, що дорівнює добутку цих чисел, було обчислено як 239500800, що відповідає отриманому програмою результату.
В лабораторній роботі було реалізовано обидва завдання, що передбачають використання власних процедур для обчислення значень функції через її вираз у ряді, а також - формул, що застосовуються в комбінаторних задачах.
Труднощі постали при програмній реалізації завдання 14.1, зокрема - у розумінні наданоїв теоретичному матеріалі формули обчислення квадратного кореня. Так, оскільки решта формул виражають функцію через суму членів ряду, аналогічний підхід було застосовано й до даної функції. Втім, кінцева реалізація все ж вірно обчислює значення функції як n-ний член ряду.
Додаткові труднощі виникли при програмній реалізації завдання 14.1 у випадку точок -1, -0.5 та 0, оскільки кінцева функція в цих точках повертає, відповідно, нескінченність або нераціональне число. В даних випадках не було можливим застосування різниці між сусідніми членами ряду для зупиники процесу, оскільки необхідної точності не вдавалось досягнути. Натомість, довелось застососувати максимальну кільість ітерацій. Втім, цілком можливим було б і застосування окремого оброблення вхідних даних, що не входять в область визначення функції квадратного кореня.