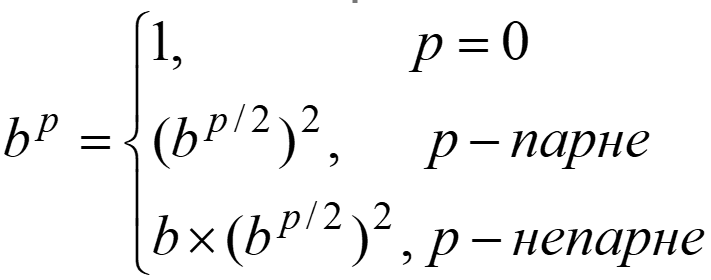Сформувати декларативне мислення в галузі програмування завдяки використанню чистих функцій, рекурсій замість циклів, запобіганню даних, що змінюються. Опанувати застосування рекурсивних функцій для обчислювальних процесів.
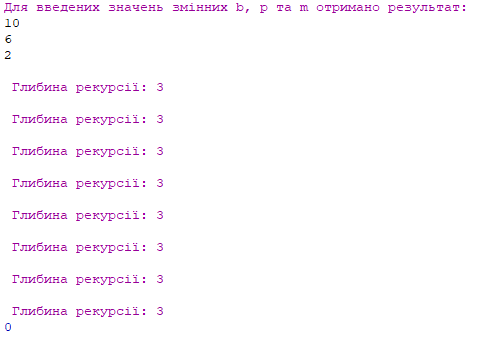
14.1. Увести з клавіатури три натуральних числа b, p, m. Обчислити значення виразу , де операція mod обраховує остачу від ділення цілих чисел. Для зведення в степень b^p з логарифмічною складністю O(log p) використати рекурентне співвідношення:
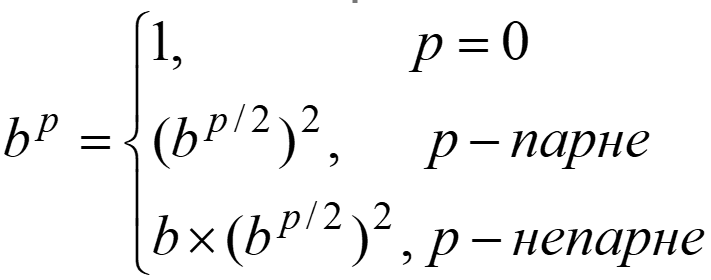
14.2. Увести з клавіатури натуральне число n. Використовуючи рекурсивну функцію, визначити і вивести всі непарні (парні) числа з послідовності цілих чисел від n до 0, зберігаючи їх порядок. Контрольний тест: введено число 8, отриманий результат: 7 5 3 1.
Для розв'язку завдання було обрано мову Scheme та середовище DrRacket. Основними критеріями, за якими було зроблено вибір, є:
Наявність доволі великої кількості довідникових джерел інформації з синтаксису та поведінки даної мови. Це, в свою чергу, забезпечено й тим, що дана мова є діалектом розповсюдженої мови - LISP.
Відносна простота даної мови у засвоєнні, а середовища - використані, завдяки зрозумілому мінімалістичному користувацьому інтерфейсу, що надає найпоширеніший функціонал для написання та відлагоджування коду.
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 1, завдання 14.1
(define (power b p depth) ; процедура піднесення до ступеня
(if (= p 0) ; умова закінчення рекурсії
(begin (display "\n Глибина рекурсії: ") (display depth) (display "\n") 1) ; виведення поточної глибини рекурсії
(if(odd? p) ; перевірка, чи є показник степеня непарним
(* b (power b (/ (- p 1) 2) (+ depth 1)) (power b (/ (- p 1) 2) (+ depth 1))) ; вираз для непарного значення
(* (power b (/ p 2) (+ depth 1)) (power b (/ p 2) (+ depth 1))) ; вираз для парного значення
)
)
)
(define (func b p m) ; процедура обчислення кінцевого виразу
(modulo (power b p 0) m)) ; обчислення модуля значення, отриманого процедурою піднесення до степеня
(display "Завдання 14.1")
(display "Для введених значень змінних b, p та m отримано результат:")
(func (read) (read) (read))
; Лавріненко В.В.
; ІПЗ-42
; Л.р. 1, завдання 14.2
(define (odd-numbers current-string current-number) ; процедура виведення всіх непарних чисел, менших за n та більших за 0
(if (= current-number 0) ; умова виходу з рекурсії
current-string ; повернення кінцевого рядкового значення
(if (odd? current-number) ; перевірка, чи є число непарним
(odd-numbers (string-append current-string (number->string current-number) " ") (- current-number 1)) ; рекурсивний виклик процедури для рядка з конткатенованим поточним значенням
; ... для наступного значення
(odd-numbers current-string (- current-number 1)) ; рекурсивний виклик процедури для незміненого рядка та наступного значення
)
)
)
(display "Завдання 14.2\n")
(display "Для введеного значення n отримано послідовність:\n")
(odd-numbers "" (read))
Завдання 14.1 Правильність виконання процедури було перевірено для вхідних даних: b = 10, p = 6, m = 2. При цьому було отримано результат, що становить 0. Перевірка онлайн - калькулятором показала аналогічний результат. Також було визначено максимальну глибину рекурсії, що становить 3.
Завдання 14.2 Правильність виконання процедури було перевірено для вхідних даних: n = 33. При цьому процедура вивела послідовність чисел: 33 31 29 27 25 23 21 19 17 15 13 11 9 7 5 3 1, - яка, вочевидь, містить всі непарні числа на проміжку від 0 до 33.
В лабораторній роботі було реалізовано обидва завдання, що передбачають застосування рекурсії, на противагу ітеративним структурами, для розв'язку поставленої задачі.
Труднощі постали при програмній реалізації завдання 14.1, оскільки надана формула не містить зменшення значення p на 1 в показнику степеня у випадку непарного значення. Проте даний недолік було швидко усунуто, а її програмну реалізацію - виправлено.